Completing the Square:
1. Consider the quadratic functions shown to on the right. Use the method of completing the square to convert each of the functions in the left-hand column from standard form to vertex form. The answers are in the right hand column.
Video Solution to a)
Video Solution to b)
Video Solution to c)
Video Solution to d)
Video Solution to e)
Video Solution to f)
Video Solution to g)
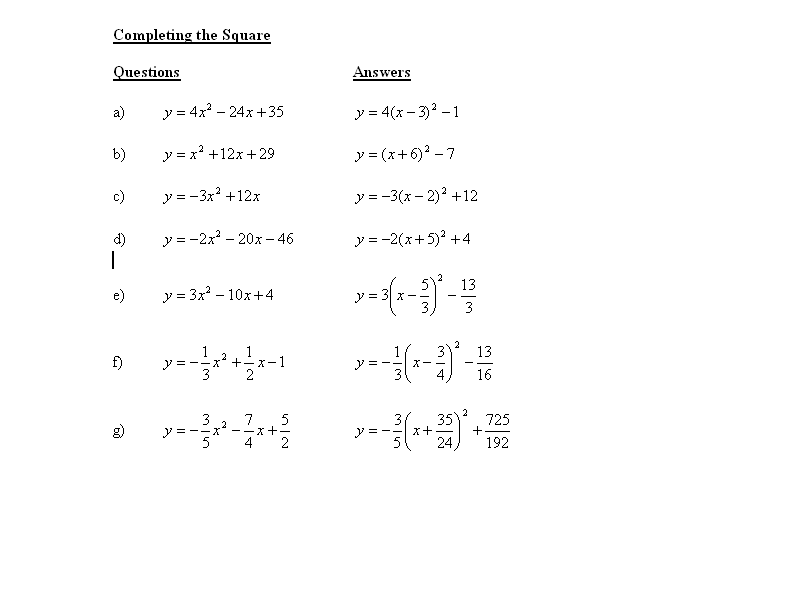
Partial Factoring:
2. Consider the quadratic functions shown on the right. Use the method of partial factoring to convert each of the functions in the left-hand column from standard form to vertex form. The answers are in the right hand column.
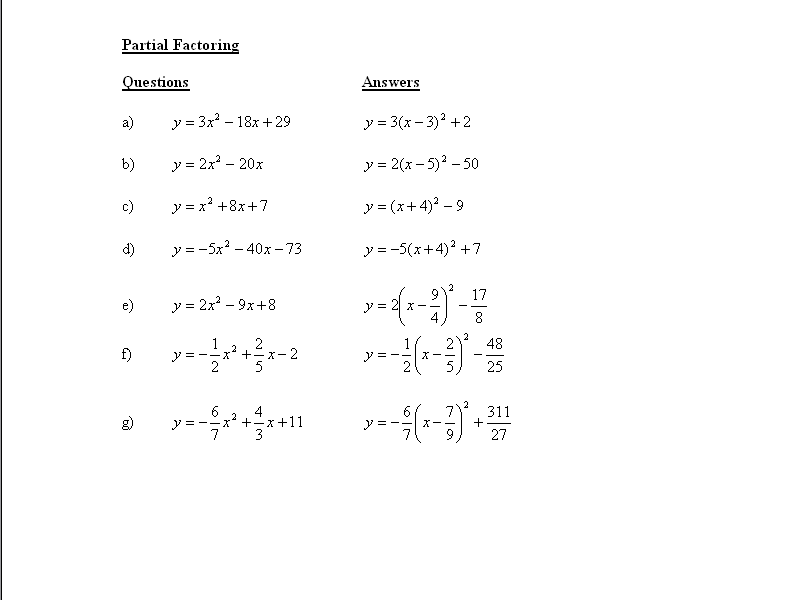
Determining the Equation if you know the vertex and another point
3. Determine the equation of a parabola in standard
form with a vertex at (-3, 5) and that passes through the point (-5, 37)
ANSWER: y = 8x^2 + 48x +
77 Video Solution to #12
Points of Intersection
4. Determine the point(s) of intersection of the
parabola y = -4x^2 + 7x + 32 and the straight line 5x + y + 8 = 0
ANSWER: (-2, 2) and (5,
-33) Video
solution to #7
Discriminant
5. Determine the number of real zeros in each of the
following cases:
a) f(x) = 19x^2 + 27x + 3
b) f(x) = 3x^2 - 24x + 48
c) f(x) = -x^2 - 6x - 11
ANSWERS: a) 2 b)
1 c)
0 Video
solution to #5
Graphing
6. Graph the curve y = -2 (x-3)^2 + 5 by first verbally stating all of the transformations that take place and then graphing in such a way that you show each of the transformations along the way, and then put your final answer in a distinctive colour.
7. Graph the curve y = 1/2 x^2 + 4x + 6 by finding the coordinates of five key points and then graphing.